Pair of Linear Equations in two variables:
Also the points for first equations are (0,10)and (10,0) 
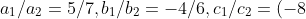/9 "a_1/a_2 =5/7,b_1/b_2 =-4/6,c_1/c_2 =(-8)/9")
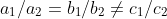
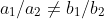
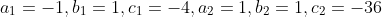
and
Linear Equations:An equation with highest power of the variable as 1 is called linear equation
ex: 2x+5=7, x+y=7, 5x=7 etc
Linear Equations in two variables:If in a linear equation there is two variables it is called as linear equation in two variable
Pair of Linear Equations in two variables: the following are some of the examples of linear equation in two variables 2x + 3y = 5
x – 2y – 3 = 0
The general form for a pair of linear equations in two variables x and y is
If we take the two of these linear equations geometrically one of the following case will be appeared (i) The two lines will intersect at one point.
(ii) The two lines will not intersect, i.e., they are parallel.
(iii) The two lines will be coincident.
Example 1 : Let us take the example given Akhila goes to a fair with ` 20 and wants to have rides on the Giant Wheel and play Hoopla. Represent this situation algebraically and graphically (geometrically).
Solution)
The pair of equations formed is :
i.e., x – 2y = 0 -----------(1)
3x + 4y = 20---------- (2)
Let us represent these equations graphically. For this, we need at least two solutions for each equation. We give these solutions in Table
Plot the points A(0, 0), B(2, 1)and P(0, 5), Q(4, 2), correspondingto the solutions in Table 3.1. Now draw the lines AB and PQ,representing the equations x – 2y = 0 and 3x + 4y = 20, as shown in Fig
the graphical representation
EXERCISE 3.1
1. Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” (Isn’t this interesting?) Represent this situation algebraically and graphically
sol)
Let the present age of Aftab be "x"years and his daughters is "y"years.
ATQ
x-7=7(y-7)-----> x-7y=-42
x+3=3(y+3)-----> x-3y=6
The graphical representation is as follows
2. The coach of a cricket team buys 3 bats and 6 balls for ` 3900. Later, she buys another bat and 3 more balls of the same kind for ` 1300. Represent this situation algebraically and geometrically.
sol)
let the price of bat be "x"rupees and ball be "y"rupees.
hence, the situation algebraically 3x+6y=3900
x+3y=1300
and, 
and points for first line is (300,500) and(100,600) for second equation(100,400) and (-200,500)
by representing graphically we get
3. The cost of 2 kg of apples and 1kg of grapes on a day was found to be ` 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is ` 300. Represent the situation algebraically and geometrically.
sol)
let the cost of one kg apple be "x"rupees and grapes be "y" rupees
ATQ the situations algebraically
2x+y=160
4x+2y=300
the solutions for the above equations are
The points for first equations are (50,60) and (80,0)
and for second equations are (60,30) and(75,0)
hence graphically
EXERCISE 3.2
1. Form the pair of linear equations in the following problems, and find their solutions graphically.
(i) 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
sol)
let the number of girls be x and and number of boys be y
ATQ x+y=10 and x-y=4
| x | 0 | 10 |
| y | 10 | 0 |
and
| x | 0 | 4 |
| y | -4 | 0 |
for second equations(0,-4)and(4,0)
The graph of the situation as follows
(ii) 5 pencils and 7 pens together cost ` 50, whereas 7 pencils and 5 pens together cost ` 46. Find the cost of one pencil and that of one pen
sol)
let cost of pencil be x rupees and pen be y rupees
According to question 5x+7y=50 and 7x+5y=46
so
and
the points for first line is (3,5) and (10,10) and for second line(8,-2) and (3,5)
| x | 3 | 10 |
| y | 5 | 0 |
| x | 8 | 3 |
| y | -2 | 5 |
the graphical representation is as follows
2. On comparing the ratios a1/a2,b1/b2 and c1/c2 , find out whether the lines representing the
following pairs of linear equations intersect at a point, are parallel or coincident
(i) 5x – 4y + 8 = 0 ,7x + 6y – 9 = 0 (ii) 9x + 3y + 12 = 0,18x + 6y + 24 = 0
(iii) 6x – 3y + 10 = 0 ,2x – y + 9 = 0
Sol)
i) Given equations 5x – 4y + 8 = 0 ,7x + 6y – 9 = 0
on comparing with
so the lines are intersecting lines
ii)Given equations 9x + 3y + 12 = 0,18x + 6y + 24 = 0
on comparing with
there fore the given line are coincidental lines
iii)Given equations6x – 3y + 10 = 0 ,2x – y + 9 = 0
on comparing with
There fore the lines are parallesl lines
4. Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
(i) x + y = 5, 2x + 2y = 10
Sol) Given equations x + y -5= 0, 2x + 2y -10= 0
on comparing with
so, the lines are coincidental lines are consistant with infinity solutions
there fore for every value of x we can get related y value.
(ii) x – y = 8, 3x – 3y = 16
Sol) Given equationsx – y -8= 0, 3x – 3y-16 =0
on comparing with
so,
therefore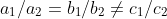
hence the lines are parallell(inconsistant) , We cannot find common solution
(iii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
Sol) Given equations 2x + y – 6 = 0, 4x – 2y – 4 = 0
on comparing with
so,
The lines are inter secting lines and consistant
2x + y – 6 = 0------->y=6-2x and
4x – 2y – 4 = 0 ------->y=2x-2
| x | 0 | 3 |
| y | 6 | 0 |
The graphical representation of these lines as follows
There for the common solution of the equation is x=2, y=2
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0
Sol) Given equations are 2x – 2y – 2 = 0, 4x – 4y – 5 = 0
on comparing with
we get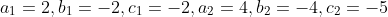 
so,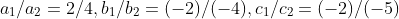 
hence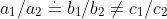 
The lines are not consistant,not possible to find common solution
5. Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
Sol) let the width of garden be X m then length will be y m
ATQ y-x=4 and x+y=36
on comparing with
so ,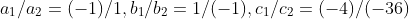 
hence,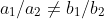
WE can find the solution
y-x=4 ------>y=x+4 and y=-36-x
| x | 0 | -4 |
| y | 4 | 0 |
| x | 0 | 36 |
| y | 36 | 0 |
the geometrical representation is
There fore the width s 16 and length is 20
6. Given the linear equation 2x + 3y – 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is:
(i) intersecting lines (ii) parallel lines (iii) coincident lines
Sol) i) 2x + 3y – 8 = 0 ii) 2x + 3y – 8 = 0 iii)2x + 3y – 8 = 0
3x+2y-8=0 2x+3y+8=0 4x+6y-16=0
7. Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.
Sol) Given equations x – y + 1 = 0
3x + 2y – 12 = 0
graphical representation of the Equations is
The vertices of the triangle is (2,3), (-1,0) and (4,0)
This is dummy text. It is not meant to be read. Accordingly, it is difficult to figure out when to end it. But then, this is dummy text. It is not meant to be read. Period.
ConversionConversion EmoticonEmoticon